Perspectivce Divide

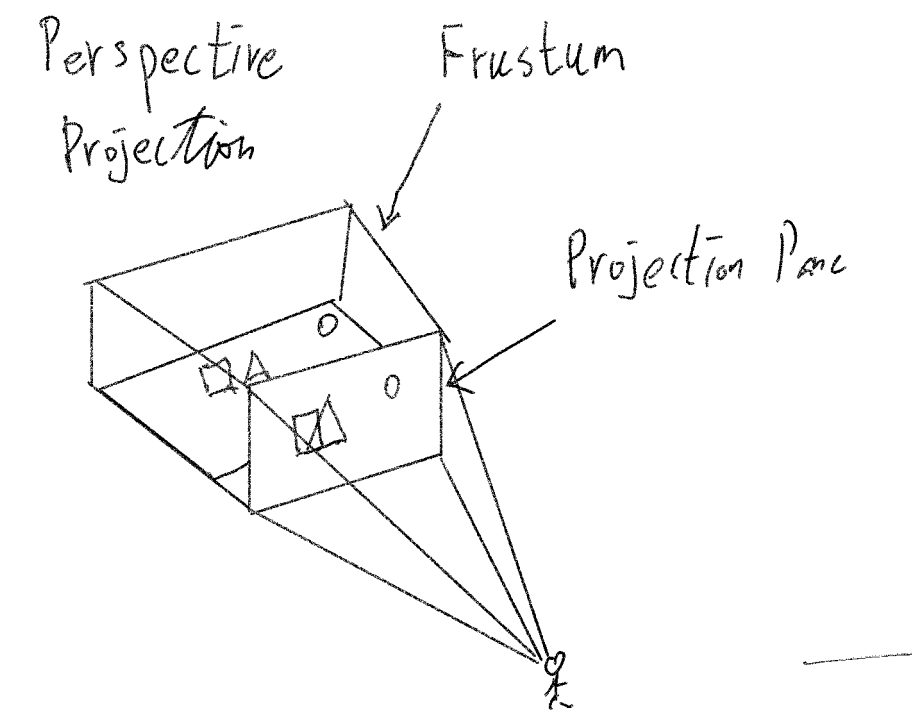
The differen with Orthographic projection , Perspectivce Projection which care about the z. Using z to represent depth.

Lets say we want to make vector P a 3D vector (x, y, z) to display on screen as vector P’(x,y) on screen.

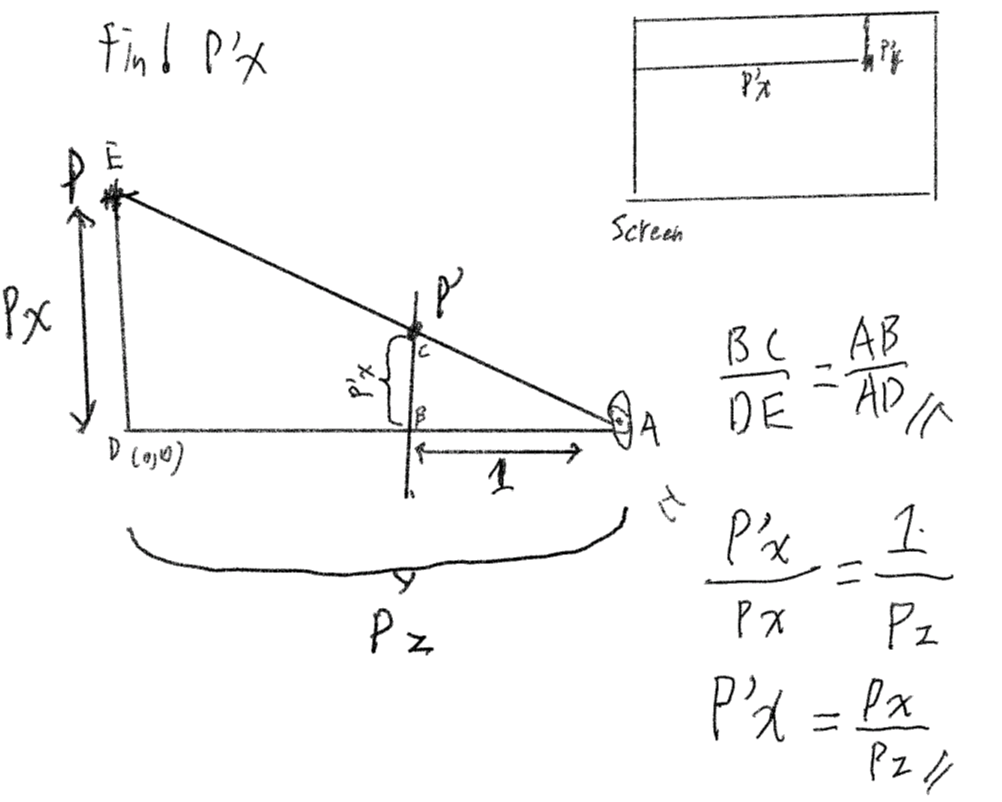
The image show that this is a similar triangle from our eye A to point P which lable e with z depth

The similar trinangle is ADE and ABC, the the similar triangle formular is:

$$ \frac{BC}{DE} = \frac{AB}{AD} $$

Replace the label as our vector value: $$ \frac{P’x}{Px} = \frac{1}{Pz} $$

Do some simple algebra make the target P’x to the left: $$ P’x = \frac{Px}{Pz} $$

Now we get the formular that how to get the x on screen.

Same as P’y here:

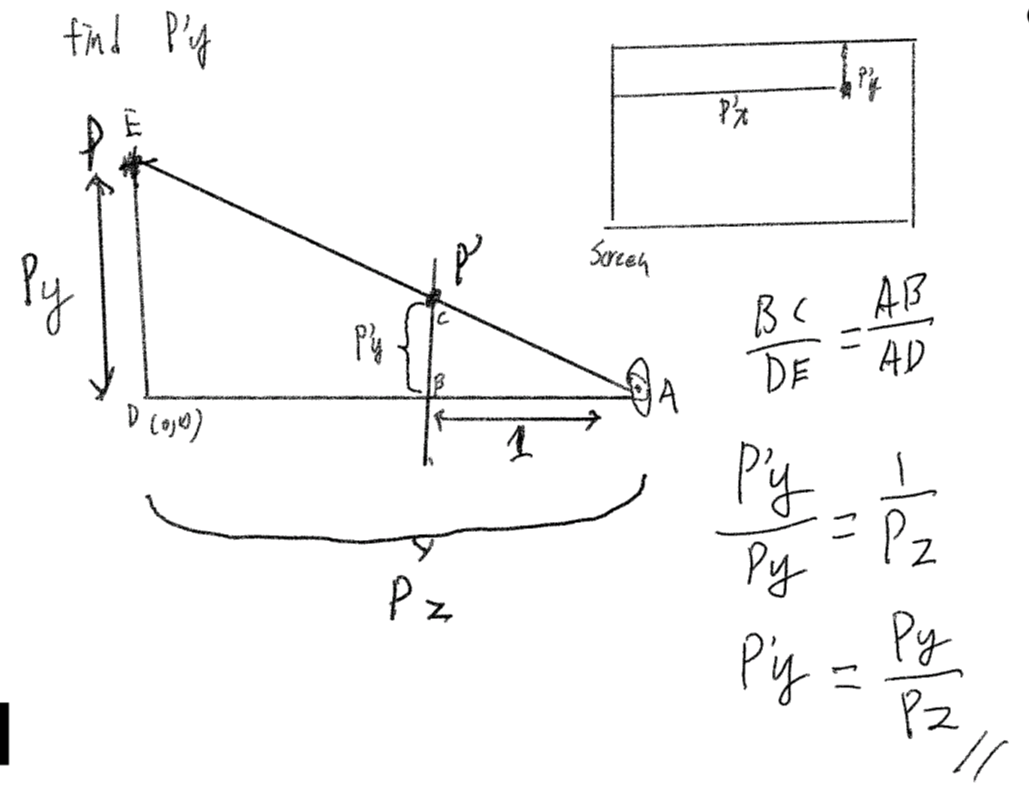
$$ \frac{BC}{DE} = \frac{AB}{AD} $$

Replace the label as our vector value: $$ \frac{P’y}{Py} = \frac{1}{Pz} $$

Do some simple algebra make the target P’y to the left: $$ P’y = \frac{Py}{Pz} $$

Finally we get a formular call prespective divide: $$ P’x = \frac{Px}{Pz} $$ $$ P’y = \frac{Py}{Pz} $$ Simple formular, but tell you the magic - The x and y is relate with z value is big or small.

implement

Define vector 3D:

typedef struct {
  float x;
  float y;
  float z;
} vec3_t;

Define a simple camera as our eyes:

vec3_t camera_position = { .x = 0, .y = 0, .z = -5 };

z = -5 for adjust the view of 3D object.

Create a 3D cube (9x9x9) as example

vec3_t cube_points[9 * 9 * 9];

for(float x = -1; x <= 1; x += 0.25) {
    for(float y = -1; y <= 1; y += 0.25) {
      for(float z = -1; z <= 1; z += 0.25) {
        vec3_t point = { .x = x, .y = y, .z = z}; // c99 format

        cube_points[point_count++] = point;
      }
    }
}

Change the project function based on above formular:

vec2_t project(vec3_t point) {
  vec2_t projected_point = {
    .x = (fov * point.x) / point.z,
    .y = (fov * point.y) / point.z
  };
  return projected_point;
}

Render the Cube:

for(int i = 0; i < (9 * 9 * 9); i++) {
    vec3_t point = cube_points[i];
    // adjust each point Z with camera.z
     point.z -= camera_position.z; 

    // Project the current point
    vec2_t projected_point = project(point);
    // Save the projected 2D vector in the array
    projected_points[i] = projected_point;
}

Result:

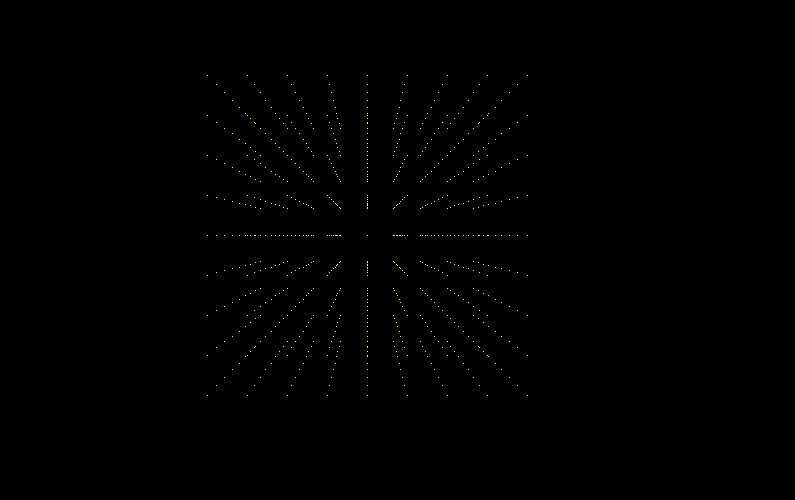
Prove that the Z can effect the X and y. We adjust the Z value on each game loop.

camera_position.z += 0.001;